Why Dan's proposal doesn't reduce payment for BPs
Article credited to jerryfane and provided by EOS GO

I did this post to clarify the concept behind Dan's proposal. This post is therefore not comparing the proposal of EOS NY and the proposal of Dan, but it's providing some interesting estimates on how staking pools could affect the inflation levels of the EOS Mainnet.
Token Holders are in control of the EOS mainnet
Since both the Governance proposals were published, I've noticed a strong misconception about how Dan's proposal is going to reduce the payment of BPs to 0.5%. This was taken as an absolute reduction in Block producers' payment, and seen in a negative way as it was stated that "BPs would never accept a reduction in their rewards, thus Dan's proposal is infeasible".
To explain why this sentence is not correct, it's important to understand that BPs are not in control of the EOS mainnet, and that the token holders have the last word. It is the token holders who can elect or remove the block producers, and by token holders I mean the largest token holders who actually have a strong influence on the block producers who are among the top 21 at present.
If these token holders understand that they can earn more (not only in economic terms) from the implementation of Dan's proposal, they will be incentivised to remove BPs that deny its activation and to vote for BPs in favour of this proposal. For this reason, we can say that BPs are only a representation of the largest token holders, otherwise they would not be part of the top 21. Consequently, it is the token holders who decide whether to implement one proposal or another, as it should be.
Staking Pools Inflation goes to the largest token holders
Given this fundamental premise, we can move on to the next step. Dan's proposal not only provides a reduction of the BPs payment to 0.5% inflation, but also provides the creation of 6 staking pools, which result in an additional inflation of 3%. The mainnet, in this case, would reach a total inflation of 3.5%. Each staking pool will have at its disposal a 0.5% of inflation to be distributed in proportion to the users who staked their EOS towards that particular staking pool. The more tokens a user staked in the staking pool, the greater the proportion of rewards that this user will receive. Since the largest token holders by definition have more tokens than the other users, this means that they will also receive a larger portion of the inflation from the staking pools. This is a key point to remember, we will need it later.
Now we have to take from Dan one the assumptions he used to define his proposal: "we can conservatively assume all accounts which vote for a producer are owned by the producer". This assumption is actually a significant one given the change in voting pattern, based on 1T1V, which makes it a very realistic assumption.
Now let's put it all together: the largest token holders will receive most of the staking pool inflation, as well as BPs specific inflation. The former, amounts to a total of 3%, while the latter amounts to 0.5%. Current BPs inflation is 1%. Do you start to see where I want to get?
How many EOS are required for the BP payment to be 1% inflation?
Since we still don't know what percentage of inflation we are talking about, let's start by doing some maths. Dan's 6 staking pools are divided according to the period in which the tokens will remain blocked. We will have:
- Staking Pool 1: 3 months
- Staking Pool 2: 6 months
- Staking Pool 3: 12 months
- Staking Pool 4: 24 months (2 years)
- Staking Pool 5: 60 months (5 years)
- Staking Pool 6: 120 months (10 years)
In the case of market equilibrium, that is in the case a new token holder is indifferent in putting 1 EOS in a staking pool (as it would bring them the same annual reward) we will have the following percentage of weights entrusted to each Staking Pool. To measure the Weight it's sufficient to make the ratio between the time in which the EOS tokens were locked and the total staking time of the Pools.
Note: for Weight I mean the ratio between the EOS staked in a Pool compared to the total number of EOS staked in all Pools.
- Staking Pool 1, Weight: 51.3%
- Staking Pool 2, Weight: 25.6%.
- Staking Pool 3, Weight: 12.8%.
- Staking Pool 4, Weight: 6.4%
- Staking Pool 5, Weight: 2.6%
- Staking Pool 6, Weight: 1.3%
With these weights, adding 1 EOS to any staking pool will give the same annual reward. This is a great way to predict how the EOS tokens will be distributed across the various staking pools.
Currently 57% of EOS have been staked in the Mainnet. Since there are a bit more than one billion EOS in circulation, we will have 570 million tokens staked. If we assume that all these tokens will be placed in a staking pool, we can calculate the total number of staked EOS for each pool:
- Staking Pool 1, Weight: 51.3%, 292.3M
- Staking Pool 2, Weight: 25.6%, 146.1M
- Staking Pool 3, Weight: 12.8%, 73.0M
- Staking Pool 4, Weight: 6.4%, 36.5M
- Staking Pool 5, Weight: 2.6%, 14.6M
- Staking Pool 6, Weight: 1.3%, 7.3M
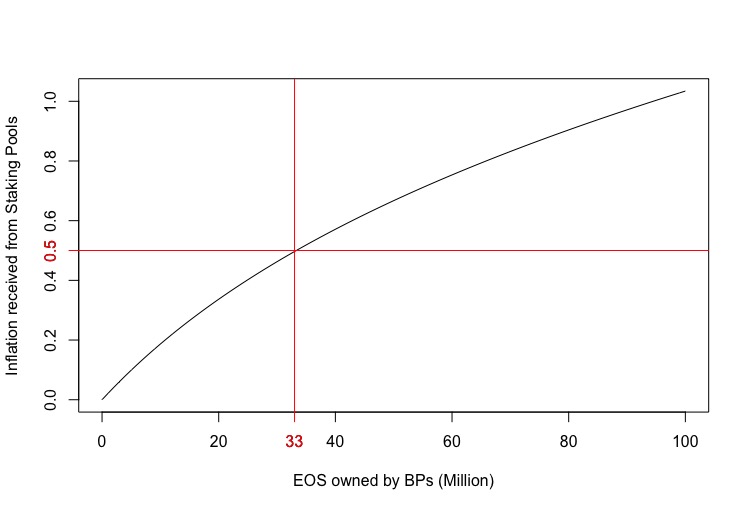
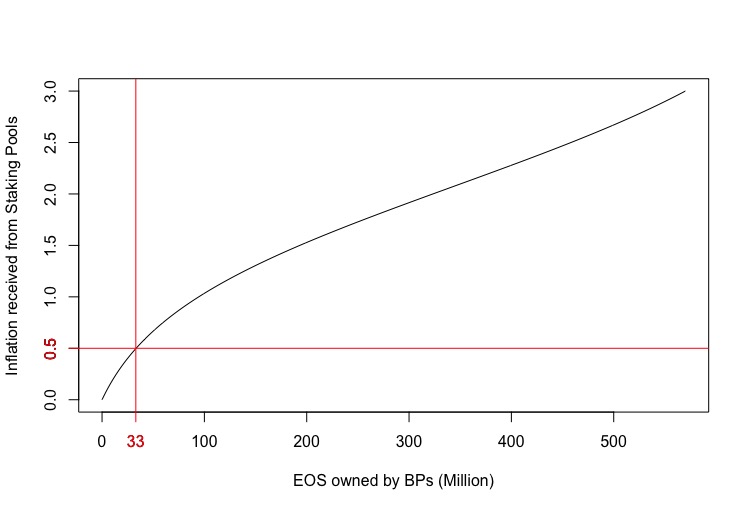
Very well, now we can understand how many EOS are needed in the Staking Pools by the Block Producers (or the largest token holders as we have assumed) to recover the 0.5% of inflation that has been removed from the pay of the BPs. In this way we will know how many EOS are enough for the rewards of the BPs to be identical to the current one.
This problem can be addressed by solving a minimization equation, which can also be done with a simple Excel spreadsheet. If we take the case in which the BPs divide their own EOS uniformly among the 6 staking pools, only 33 million EOS will be enough to recover the 0,5% of annual inflation. We will then know that, for every staking pool, the BPs will set in stake 33/6 = 5.5M of EOS. This will allow them to own:
- 1.96% of the Staking Pool 1
- 3.84% of the Staking Pool 2
- 7.40% of the Staking Pool 3
- 13.78% of the Staking Pool 4
- 28.54% of the Staking Pool 5
- 44.41% of the Staking Pool 6
This will reduce the risks for BPs, while ensuring 0.5% inflation. 33 million EOS corresponds to only 5.79% of the total EOS staked. In my opinion, most staked EOS are currently held by a fair number of token holders, which means that 33M is a very low number. However, it would allow the same level of current inflation to be reached. Potentially, the BPs (which by assumption are equivalent to the largest token holders), through Dan's proposal will receive a higher payout than the current system and not a lower payout.
The formula below measures the inflation received by BPs from staking pools by the number of EOS that the BPs jointly hold.
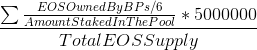
The following chart corresponds to the above function, we can see that with 33 million EOS held by BPs, they will be able to receive 0.5% inflation from staking pools.
Disclaimer: The views expressed by the author above do not necessarily represent the views of EOS GO. EOS GO is a community where EOS GO Blog being a platform for authors to express their diverse ideas and perspectives. Any referral links present were placed directly by the author, from which EOS Go does not derive any benefits. To learn more about EOS GO and EOS, please join us on our social medias.
EOS GO is funded by EOS ASIA and powered by YOU. Join the community and begin contributing to the movement by adding eos go to your name and joining the EOS GO telegram group.